Spline Flow Regression¶
Normalizing flows transform a simple distribution into a complex data distribution through a series of invertible transformations. The key steps involved in the operation of normalizing flows are as follows (from left to right):
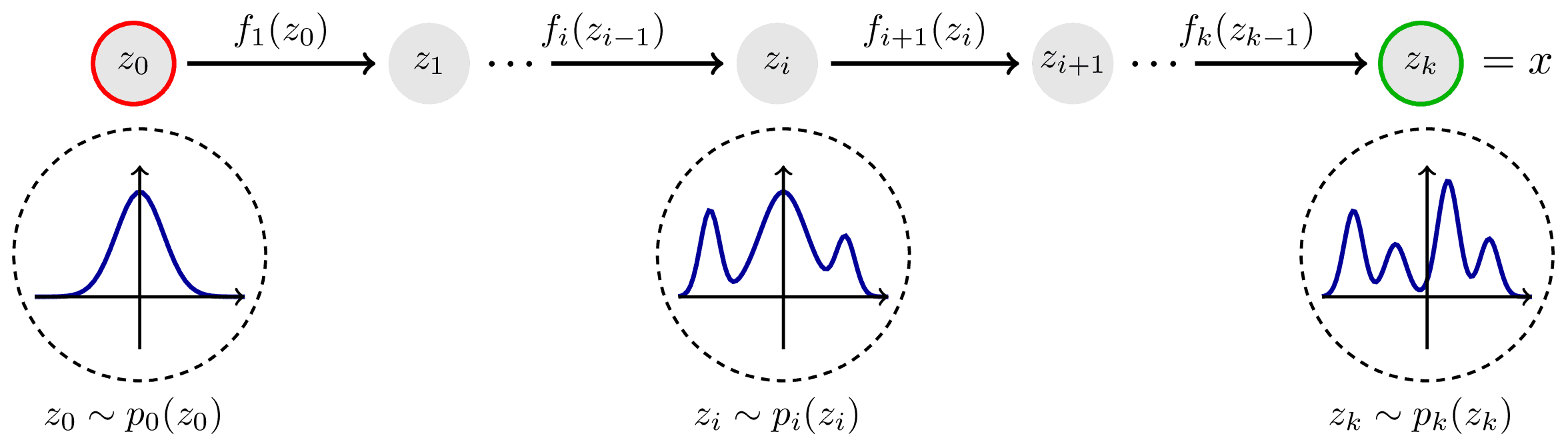
Image source: https://tikz.net/janosh/normalizing-flow.png
- Start with a simple, easy-to-sample distribution, usually a Gaussian, which serves as the "base" distribution
- Apply a series of invertible transformations to map the samples from the base distribution to the desired complex data distribution
- Each transformation in the flow must be reversible, meaning it has both a forward pass (sampling from the base distribution to the complex distribution) and an inverse pass (mapping samples from the complex distribution back to the base distribution)
- The flow ensures that the probability density function (PDF) of the complex distribution can be analytically calculated using the determinant of the Jacobian matrix resulting from the transformations
By stacking multiple transformations in a sequence, normalizing flows can model complex and multi-modal distributions while providing the ability to compute the likelihood of the data and perform efficient sampling in both directions (from base to complex and vice versa). However, it is important to note that since LightGBMLSS is based on a one vs. all estimation strategy, where a separate tree is grown for each parameter, estimating many parameters for a large dataset can become computationally expensive. For more details, we refer to our related paper Alexander März and Thomas Kneib (2022): Distributional Gradient Boosting Machines.
Imports¶
In [1]:
Copied!
from lightgbmlss.model import *
from lightgbmlss.distributions.SplineFlow import *
from lightgbmlss.distributions.flow_utils import NormalizingFlowClass
from lightgbmlss.datasets.data_loader import load_simulated_gaussian_data
from scipy.stats import norm
import plotnine
from plotnine import *
plotnine.options.figure_size = (20, 10)
from lightgbmlss.model import *
from lightgbmlss.distributions.SplineFlow import *
from lightgbmlss.distributions.flow_utils import NormalizingFlowClass
from lightgbmlss.datasets.data_loader import load_simulated_gaussian_data
from scipy.stats import norm
import plotnine
from plotnine import *
plotnine.options.figure_size = (20, 10)
Data¶
In [2]:
Copied!
# The data is simulated as a Gaussian, where x is the only true feature and all others are noise variables
# loc = 10
# scale = 1 + 4 * ((0.3 < x) & (x < 0.5)) + 2 * (x > 0.7)
train, test = load_simulated_gaussian_data()
X_train, y_train = train.filter(regex="x"), train["y"].values
X_test, y_test = test.filter(regex="x"), test["y"].values
dtrain = lgb.Dataset(X_train, label=y_train)
# The data is simulated as a Gaussian, where x is the only true feature and all others are noise variables
# loc = 10
# scale = 1 + 4 * ((0.3 < x) & (x < 0.5)) + 2 * (x > 0.7)
train, test = load_simulated_gaussian_data()
X_train, y_train = train.filter(regex="x"), train["y"].values
X_test, y_test = test.filter(regex="x"), test["y"].values
dtrain = lgb.Dataset(X_train, label=y_train)
Select Normalizing Flow¶
In the following, we specify a list of candidate normalizing flows. The function flow_select returns the negative log-likelihood of each specification. The normalizing flow with the lowest negative log-likelihood is selected. The function also plots the density of the target variable and the fitted density, using the best suitable normalizing flow among the specified ones. However, note that choosing the best performing flow based solely on training data may lead to overfitting, since normalizing flows have a higher risk of overfitting compared to parametric distributions. When using normalizing flows, it is crucial to carefully select the specifications to strike a balance between model complexity and generalization ability.
In [3]:
Copied!
# See ?SplineFlow for an overview.
bound = np.max([np.abs(y_train.min()), y_train.max()])
target_support = "real"
candidate_flows = [
SplineFlow(target_support=target_support, count_bins=2, bound=bound, order="linear"),
SplineFlow(target_support=target_support, count_bins=4, bound=bound, order="linear"),
SplineFlow(target_support=target_support, count_bins=6, bound=bound, order="linear"),
SplineFlow(target_support=target_support, count_bins=8, bound=bound, order="linear"),
SplineFlow(target_support=target_support, count_bins=12, bound=bound, order="linear"),
SplineFlow(target_support=target_support, count_bins=16, bound=bound, order="linear"),
SplineFlow(target_support=target_support, count_bins=20, bound=bound, order="linear"),
SplineFlow(target_support=target_support, count_bins=2, bound=bound, order="quadratic"),
SplineFlow(target_support=target_support, count_bins=4, bound=bound, order="quadratic"),
SplineFlow(target_support=target_support, count_bins=6, bound=bound, order="quadratic"),
SplineFlow(target_support=target_support, count_bins=8, bound=bound, order="quadratic"),
SplineFlow(target_support=target_support, count_bins=12, bound=bound, order="quadratic"),
SplineFlow(target_support=target_support, count_bins=16, bound=bound, order="quadratic"),
SplineFlow(target_support=target_support, count_bins=20, bound=bound, order="quadratic"),
]
flow_nll = NormalizingFlowClass().flow_select(target=y_train, candidate_flows=candidate_flows, max_iter=50, n_samples=10000, plot=True, figure_size=(12, 5))
flow_nll
# See ?SplineFlow for an overview.
bound = np.max([np.abs(y_train.min()), y_train.max()])
target_support = "real"
candidate_flows = [
SplineFlow(target_support=target_support, count_bins=2, bound=bound, order="linear"),
SplineFlow(target_support=target_support, count_bins=4, bound=bound, order="linear"),
SplineFlow(target_support=target_support, count_bins=6, bound=bound, order="linear"),
SplineFlow(target_support=target_support, count_bins=8, bound=bound, order="linear"),
SplineFlow(target_support=target_support, count_bins=12, bound=bound, order="linear"),
SplineFlow(target_support=target_support, count_bins=16, bound=bound, order="linear"),
SplineFlow(target_support=target_support, count_bins=20, bound=bound, order="linear"),
SplineFlow(target_support=target_support, count_bins=2, bound=bound, order="quadratic"),
SplineFlow(target_support=target_support, count_bins=4, bound=bound, order="quadratic"),
SplineFlow(target_support=target_support, count_bins=6, bound=bound, order="quadratic"),
SplineFlow(target_support=target_support, count_bins=8, bound=bound, order="quadratic"),
SplineFlow(target_support=target_support, count_bins=12, bound=bound, order="quadratic"),
SplineFlow(target_support=target_support, count_bins=16, bound=bound, order="quadratic"),
SplineFlow(target_support=target_support, count_bins=20, bound=bound, order="quadratic"),
]
flow_nll = NormalizingFlowClass().flow_select(target=y_train, candidate_flows=candidate_flows, max_iter=50, n_samples=10000, plot=True, figure_size=(12, 5))
flow_nll
Fitting of candidate normalizing flows completed: 100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 14/14 [01:20<00:00, 5.78s/it]
Out[3]:
| nll | NormFlow | |
|---|---|---|
| rank | ||
| 1 | 16595.917006 | SplineFlow(count_bins: 20, order: linear) |
| 2 | 16608.693807 | SplineFlow(count_bins: 12, order: quadratic) |
| 3 | 16622.862265 | SplineFlow(count_bins: 16, order: quadratic) |
| 4 | 16640.156074 | SplineFlow(count_bins: 6, order: linear) |
| 5 | 16640.611035 | SplineFlow(count_bins: 16, order: linear) |
| 6 | 16649.404709 | SplineFlow(count_bins: 8, order: linear) |
| 7 | 16651.375456 | SplineFlow(count_bins: 8, order: quadratic) |
| 8 | 16653.378393 | SplineFlow(count_bins: 6, order: quadratic) |
| 9 | 16674.331780 | SplineFlow(count_bins: 12, order: linear) |
| 10 | 16822.629927 | SplineFlow(count_bins: 4, order: quadratic) |
| 11 | 16902.398862 | SplineFlow(count_bins: 20, order: quadratic) |
| 12 | 17538.588405 | SplineFlow(count_bins: 4, order: linear) |
| 13 | 17692.968508 | SplineFlow(count_bins: 2, order: linear) |
| 14 | 17737.569055 | SplineFlow(count_bins: 2, order: quadratic) |
Normalizing Flow Specification¶
Even though SplineFlow(count_bins: 20, order: linear) shows the best fit to the data, we choose a more parameter parsimonious specification (recall that a separate tree is grown for each parameter):
- for count_bins=20, we need to estimate 3*count_bins + (count_bins-1) = 79 parameters
- for count_bins=8, we need to estimate 3*count_bins + (count_bins-1) = 31 parameters
In [5]:
Copied!
# Specifies Spline-Flow. See ?SplineFlow for an overview.
bound = np.max([np.abs(y_train.min()), y_train.max()])
lgblss = LightGBMLSS(
SplineFlow(target_support="real", # Specifies the support of the target. Options are "real", "positive", "positive_integer" or "unit_interval"
count_bins=8, # The number of segments comprising the spline.
bound=bound, # By adjusting the value, you can control the size of the bounding box and consequently control the range of inputs that the spline transform operates on.
order="linear", # The order of the spline. Options are "linear" or "quadratic".
stabilization="None", # Options are "None", "MAD" or "L2".
loss_fn="nll" # Loss function. Options are "nll" (negative log-likelihood) or "crps"(continuous ranked probability score).
)
)
# Specifies Spline-Flow. See ?SplineFlow for an overview.
bound = np.max([np.abs(y_train.min()), y_train.max()])
lgblss = LightGBMLSS(
SplineFlow(target_support="real", # Specifies the support of the target. Options are "real", "positive", "positive_integer" or "unit_interval"
count_bins=8, # The number of segments comprising the spline.
bound=bound, # By adjusting the value, you can control the size of the bounding box and consequently control the range of inputs that the spline transform operates on.
order="linear", # The order of the spline. Options are "linear" or "quadratic".
stabilization="None", # Options are "None", "MAD" or "L2".
loss_fn="nll" # Loss function. Options are "nll" (negative log-likelihood) or "crps"(continuous ranked probability score).
)
)
Hyper-Parameter Optimization¶
Any LightGBM hyperparameter can be tuned, where the structure of the parameter dictionary needs to be as follows:
- Float/Int sample_type
- {"param_name": ["sample_type", low, high, log]}
- sample_type: str, Type of sampling, e.g., "float" or "int"
- low: int, Lower endpoint of the range of suggested values
- high: int, Upper endpoint of the range of suggested values
- log: bool, Flag to sample the value from the log domain or not
- Example: {"eta": "float", low=1e-5, high=1, log=True]}
- Categorical sample_type
- {"param_name": ["sample_type", ["choice1", "choice2", "choice3", "..."]]}
- sample_type: str, Type of sampling, either "categorical"
- choice1, choice2, choice3, ...: str, Possible choices for the parameter
- Example: {"boosting": ["categorical", ["gbdt", "dart"]]}
- For parameters without tunable choice (this is needed if tree_method = "gpu_hist" and gpu_id needs to be specified)
- {"param_name": ["none", [value]]},
- param_name: str, Name of the parameter
- value: int, Value of the parameter
- Example: {"gpu_id": ["none", [0]]}In [6]:
Copied!
param_dict = {
"eta": ["float", {"low": 1e-5, "high": 1, "log": True}],
"max_depth": ["int", {"low": 1, "high": 10, "log": False}],
"num_leaves": ["int", {"low": 255, "high": 255, "log": False}], # set to constant for this example
"min_data_in_leaf": ["int", {"low": 20, "high": 20, "log": False}], # set to constant for this example
"min_gain_to_split": ["float", {"low": 1e-8, "high": 40, "log": False}],
"min_sum_hessian_in_leaf": ["float", {"low": 1e-8, "high": 500, "log": True}],
"subsample": ["float", {"low": 0.2, "high": 1.0, "log": False}],
"feature_fraction": ["float", {"low": 0.2, "high": 1.0, "log": False}],
"boosting": ["categorical", ["gbdt"]],
}
np.random.seed(123)
opt_param = lgblss.hyper_opt(param_dict,
dtrain,
num_boost_round=100, # Number of boosting iterations.
nfold=5, # Number of cv-folds.
early_stopping_rounds=20, # Number of early-stopping rounds
max_minutes=1000, # Time budget in minutes, i.e., stop study after the given number of minutes.
n_trials=50, # The number of trials. If this argument is set to None, there is no limitation on the number of trials.
silence=False, # Controls the verbosity of the trail, i.e., user can silence the outputs of the trail.
seed=123, # Seed used to generate cv-folds.
hp_seed=None # Seed for random number generator used in the Bayesian hyperparameter search.
)
param_dict = {
"eta": ["float", {"low": 1e-5, "high": 1, "log": True}],
"max_depth": ["int", {"low": 1, "high": 10, "log": False}],
"num_leaves": ["int", {"low": 255, "high": 255, "log": False}], # set to constant for this example
"min_data_in_leaf": ["int", {"low": 20, "high": 20, "log": False}], # set to constant for this example
"min_gain_to_split": ["float", {"low": 1e-8, "high": 40, "log": False}],
"min_sum_hessian_in_leaf": ["float", {"low": 1e-8, "high": 500, "log": True}],
"subsample": ["float", {"low": 0.2, "high": 1.0, "log": False}],
"feature_fraction": ["float", {"low": 0.2, "high": 1.0, "log": False}],
"boosting": ["categorical", ["gbdt"]],
}
np.random.seed(123)
opt_param = lgblss.hyper_opt(param_dict,
dtrain,
num_boost_round=100, # Number of boosting iterations.
nfold=5, # Number of cv-folds.
early_stopping_rounds=20, # Number of early-stopping rounds
max_minutes=1000, # Time budget in minutes, i.e., stop study after the given number of minutes.
n_trials=50, # The number of trials. If this argument is set to None, there is no limitation on the number of trials.
silence=False, # Controls the verbosity of the trail, i.e., user can silence the outputs of the trail.
seed=123, # Seed used to generate cv-folds.
hp_seed=None # Seed for random number generator used in the Bayesian hyperparameter search.
)
[I 2023-08-11 12:37:41,890] A new study created in memory with name: LightGBMLSS Hyper-Parameter Optimization
0%| | 0/50 [00:00<?, ?it/s]
[I 2023-08-11 12:38:01,301] Trial 0 finished with value: 367804.0625 and parameters: {'eta': 0.010375304627985965, 'max_depth': 7, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 30.21888913980533, 'min_sum_hessian_in_leaf': 5.864939907646467e-06, 'subsample': 0.658481420114019, 'feature_fraction': 0.9114946619928868, 'boosting': 'gbdt'}. Best is trial 0 with value: 367804.0625.
[I 2023-08-11 12:38:15,005] Trial 1 finished with value: 327890.15625 and parameters: {'eta': 5.3460212858136167e-05, 'max_depth': 6, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 22.51771738796101, 'min_sum_hessian_in_leaf': 3.782715103966255e-06, 'subsample': 0.8565244625430195, 'feature_fraction': 0.8120123399840897, 'boosting': 'gbdt'}. Best is trial 1 with value: 327890.15625.
[I 2023-08-11 12:38:55,787] Trial 2 finished with value: 3321.39404296875 and parameters: {'eta': 2.778156946755216e-05, 'max_depth': 3, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 30.563335570212864, 'min_sum_hessian_in_leaf': 0.018998048940462937, 'subsample': 0.5982826614247189, 'feature_fraction': 0.9178957649663875, 'boosting': 'gbdt'}. Best is trial 2 with value: 3321.39404296875.
[I 2023-08-11 12:39:41,746] Trial 3 finished with value: 3264.73486328125 and parameters: {'eta': 0.00016286470418944287, 'max_depth': 8, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 0.010186033781953225, 'min_sum_hessian_in_leaf': 0.0320584443452124, 'subsample': 0.521567388874646, 'feature_fraction': 0.6273169259837587, 'boosting': 'gbdt'}. Best is trial 3 with value: 3264.73486328125.
[I 2023-08-11 12:39:51,741] Trial 4 finished with value: 376967.6875 and parameters: {'eta': 1.5684870736165636e-05, 'max_depth': 8, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 33.8874711080051, 'min_sum_hessian_in_leaf': 1.8783327364128395e-08, 'subsample': 0.8823849618907202, 'feature_fraction': 0.7045235387891493, 'boosting': 'gbdt'}. Best is trial 3 with value: 3264.73486328125.
[I 2023-08-11 12:40:02,153] Trial 5 finished with value: 398357.78125 and parameters: {'eta': 0.5548705152962901, 'max_depth': 8, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 13.667421918402665, 'min_sum_hessian_in_leaf': 4.6972881363604445e-07, 'subsample': 0.20226750190291407, 'feature_fraction': 0.6190150789735767, 'boosting': 'gbdt'}. Best is trial 3 with value: 3264.73486328125.
[I 2023-08-11 12:40:12,081] Trial 6 finished with value: 400577.875 and parameters: {'eta': 0.1234951759976552, 'max_depth': 9, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 33.13372404468565, 'min_sum_hessian_in_leaf': 1.2261575574099422e-07, 'subsample': 0.940693907349371, 'feature_fraction': 0.9449458870167231, 'boosting': 'gbdt'}. Best is trial 3 with value: 3264.73486328125.
[I 2023-08-11 12:40:52,496] Trial 7 finished with value: 142739.59375 and parameters: {'eta': 0.0003413864481981204, 'max_depth': 4, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 22.366955613110136, 'min_sum_hessian_in_leaf': 6.002551849974542e-05, 'subsample': 0.6991813218844587, 'feature_fraction': 0.234857420886585, 'boosting': 'gbdt'}. Best is trial 3 with value: 3264.73486328125.
[I 2023-08-11 12:41:01,002] Trial 8 finished with value: 365344.75 and parameters: {'eta': 0.00020409810478252383, 'max_depth': 1, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 36.855824335790395, 'min_sum_hessian_in_leaf': 1.2378209039169021e-08, 'subsample': 0.770484341624629, 'feature_fraction': 0.5551457106408251, 'boosting': 'gbdt'}. Best is trial 3 with value: 3264.73486328125.
[I 2023-08-11 12:41:40,436] Trial 9 finished with value: 3135.341064453125 and parameters: {'eta': 0.015236694462247857, 'max_depth': 2, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 19.349498338142997, 'min_sum_hessian_in_leaf': 56.443023006446865, 'subsample': 0.7640980691353356, 'feature_fraction': 0.41488213555402687, 'boosting': 'gbdt'}. Best is trial 9 with value: 3135.341064453125.
[I 2023-08-11 12:41:55,509] Trial 10 pruned. Trial was pruned at iteration 36.
[I 2023-08-11 12:42:12,555] Trial 11 pruned. Trial was pruned at iteration 36.
[I 2023-08-11 12:42:56,725] Trial 12 finished with value: 3256.26220703125 and parameters: {'eta': 0.0018049878745409515, 'max_depth': 4, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 3.374230470458916, 'min_sum_hessian_in_leaf': 0.0530979406814048, 'subsample': 0.4960846397538058, 'feature_fraction': 0.40371528463535267, 'boosting': 'gbdt'}. Best is trial 9 with value: 3135.341064453125.
[I 2023-08-11 12:43:10,887] Trial 13 pruned. Trial was pruned at iteration 32.
[I 2023-08-11 12:43:55,548] Trial 14 finished with value: 3212.943359375 and parameters: {'eta': 0.025859495137694966, 'max_depth': 4, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 6.685774705475238, 'min_sum_hessian_in_leaf': 222.98371851641804, 'subsample': 0.7995471962331264, 'feature_fraction': 0.47768677368077295, 'boosting': 'gbdt'}. Best is trial 9 with value: 3135.341064453125.
[I 2023-08-11 12:44:03,829] Trial 15 finished with value: 3329.883544921875 and parameters: {'eta': 0.03539939269416217, 'max_depth': 2, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 9.188990720570771, 'min_sum_hessian_in_leaf': 488.0785240623253, 'subsample': 0.7894909220530997, 'feature_fraction': 0.5151030280739416, 'boosting': 'gbdt'}. Best is trial 9 with value: 3135.341064453125.
[I 2023-08-11 12:44:43,469] Trial 16 finished with value: 3026.395263671875 and parameters: {'eta': 0.07594812682515821, 'max_depth': 5, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 17.792180133102768, 'min_sum_hessian_in_leaf': 22.17210994438013, 'subsample': 0.776822951588817, 'feature_fraction': 0.2890728975559498, 'boosting': 'gbdt'}. Best is trial 16 with value: 3026.395263671875.
[I 2023-08-11 12:45:09,701] Trial 17 finished with value: 3024.16162109375 and parameters: {'eta': 0.14050335876069467, 'max_depth': 5, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 17.26511630421208, 'min_sum_hessian_in_leaf': 8.270011184858163, 'subsample': 0.9896356934682706, 'feature_fraction': 0.24430206777352248, 'boosting': 'gbdt'}. Best is trial 17 with value: 3024.16162109375.
[I 2023-08-11 12:45:29,462] Trial 18 finished with value: 3172.02294921875 and parameters: {'eta': 0.7236262880129627, 'max_depth': 6, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 26.302808049098353, 'min_sum_hessian_in_leaf': 4.65621731262215, 'subsample': 0.9798594849561478, 'feature_fraction': 0.21013091104429663, 'boosting': 'gbdt'}. Best is trial 17 with value: 3024.16162109375.
[I 2023-08-11 12:46:09,170] Trial 19 finished with value: 3030.934326171875 and parameters: {'eta': 0.11541934708482965, 'max_depth': 5, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 17.39372679689958, 'min_sum_hessian_in_leaf': 0.4875471297011469, 'subsample': 0.8735372230489282, 'feature_fraction': 0.29512485474393757, 'boosting': 'gbdt'}. Best is trial 17 with value: 3024.16162109375.
[I 2023-08-11 12:46:49,777] Trial 20 finished with value: 3013.43505859375 and parameters: {'eta': 0.10851774600973758, 'max_depth': 5, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 12.778099763813188, 'min_sum_hessian_in_leaf': 19.409084894454672, 'subsample': 0.9906733215538556, 'feature_fraction': 0.31427354411349523, 'boosting': 'gbdt'}. Best is trial 20 with value: 3013.43505859375.
[I 2023-08-11 12:47:31,244] Trial 21 finished with value: 3020.79150390625 and parameters: {'eta': 0.10941312206423358, 'max_depth': 5, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 12.955452035644882, 'min_sum_hessian_in_leaf': 34.43299195414659, 'subsample': 0.993865946118584, 'feature_fraction': 0.29169024300447044, 'boosting': 'gbdt'}. Best is trial 20 with value: 3013.43505859375.
[I 2023-08-11 12:47:54,911] Trial 22 finished with value: 3017.7353515625 and parameters: {'eta': 0.27099448628298356, 'max_depth': 6, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 12.164474712430403, 'min_sum_hessian_in_leaf': 41.68415304679111, 'subsample': 0.9980808126058845, 'feature_fraction': 0.3153447935530275, 'boosting': 'gbdt'}. Best is trial 20 with value: 3013.43505859375.
[I 2023-08-11 12:48:20,851] Trial 23 finished with value: 3019.21435546875 and parameters: {'eta': 0.30191668351694284, 'max_depth': 7, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 11.917898671607471, 'min_sum_hessian_in_leaf': 44.28300751774489, 'subsample': 0.9273319278552463, 'feature_fraction': 0.3276698697022868, 'boosting': 'gbdt'}. Best is trial 20 with value: 3013.43505859375.
[I 2023-08-11 12:48:29,020] Trial 24 pruned. Trial was pruned at iteration 20.
[I 2023-08-11 12:48:50,180] Trial 25 finished with value: 3018.3837890625 and parameters: {'eta': 0.3692147736260462, 'max_depth': 7, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 10.83827075251106, 'min_sum_hessian_in_leaf': 54.98180387829638, 'subsample': 0.9355321657142412, 'feature_fraction': 0.3542729437699873, 'boosting': 'gbdt'}. Best is trial 20 with value: 3013.43505859375.
[I 2023-08-11 12:48:58,960] Trial 26 pruned. Trial was pruned at iteration 20.
[I 2023-08-11 12:49:07,470] Trial 27 pruned. Trial was pruned at iteration 20.
[I 2023-08-11 12:49:20,520] Trial 28 pruned. Trial was pruned at iteration 32.
[I 2023-08-11 12:49:36,017] Trial 29 pruned. Trial was pruned at iteration 38.
[I 2023-08-11 12:49:52,087] Trial 30 pruned. Trial was pruned at iteration 39.
[I 2023-08-11 12:50:24,408] Trial 31 finished with value: 3019.494873046875 and parameters: {'eta': 0.2725991488316807, 'max_depth': 7, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 11.759315835515839, 'min_sum_hessian_in_leaf': 26.987460432181546, 'subsample': 0.998147928571545, 'feature_fraction': 0.32559028682493446, 'boosting': 'gbdt'}. Best is trial 20 with value: 3013.43505859375.
[I 2023-08-11 12:50:43,988] Trial 32 finished with value: 3015.494140625 and parameters: {'eta': 0.3829501207030448, 'max_depth': 6, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 10.006822682462404, 'min_sum_hessian_in_leaf': 9.670757510705382, 'subsample': 0.9424904465703395, 'feature_fraction': 0.3111946445504374, 'boosting': 'gbdt'}. Best is trial 20 with value: 3013.43505859375.
[I 2023-08-11 12:50:52,661] Trial 33 pruned. Trial was pruned at iteration 20.
[I 2023-08-11 12:51:33,990] Trial 34 finished with value: 3005.75537109375 and parameters: {'eta': 0.06012752850837495, 'max_depth': 6, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 5.803902946638742, 'min_sum_hessian_in_leaf': 2.3261118096334563, 'subsample': 0.9482108811109413, 'feature_fraction': 0.41287326458142043, 'boosting': 'gbdt'}. Best is trial 34 with value: 3005.75537109375.
[I 2023-08-11 12:52:15,466] Trial 35 finished with value: 3000.99462890625 and parameters: {'eta': 0.06943267180218958, 'max_depth': 4, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 4.133726741234719, 'min_sum_hessian_in_leaf': 1.7385973286087377, 'subsample': 0.8908962112260067, 'feature_fraction': 0.42160506776781076, 'boosting': 'gbdt'}. Best is trial 35 with value: 3000.99462890625.
[I 2023-08-11 12:52:26,240] Trial 36 pruned. Trial was pruned at iteration 24.
[I 2023-08-11 12:52:36,406] Trial 37 pruned. Trial was pruned at iteration 24.
[I 2023-08-11 12:52:45,020] Trial 38 pruned. Trial was pruned at iteration 21.
[I 2023-08-11 12:52:53,486] Trial 39 pruned. Trial was pruned at iteration 20.
[I 2023-08-11 12:53:02,563] Trial 40 pruned. Trial was pruned at iteration 21.
[I 2023-08-11 12:53:41,543] Trial 41 finished with value: 3005.391845703125 and parameters: {'eta': 0.15498347493908707, 'max_depth': 4, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 7.365763456361323, 'min_sum_hessian_in_leaf': 12.723870730914529, 'subsample': 0.9556994060266463, 'feature_fraction': 0.3792850237470474, 'boosting': 'gbdt'}. Best is trial 35 with value: 3000.99462890625.
[I 2023-08-11 12:54:21,491] Trial 42 finished with value: 3007.25048828125 and parameters: {'eta': 0.1548185495847896, 'max_depth': 4, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 7.156358312749202, 'min_sum_hessian_in_leaf': 9.06469298926148, 'subsample': 0.9562432564521889, 'feature_fraction': 0.3674839079182071, 'boosting': 'gbdt'}. Best is trial 35 with value: 3000.99462890625.
[I 2023-08-11 12:54:29,988] Trial 43 pruned. Trial was pruned at iteration 20.
[I 2023-08-11 12:54:38,844] Trial 44 pruned. Trial was pruned at iteration 21.
[I 2023-08-11 12:54:47,767] Trial 45 pruned. Trial was pruned at iteration 20.
[I 2023-08-11 12:54:56,168] Trial 46 pruned. Trial was pruned at iteration 20.
[I 2023-08-11 12:55:23,650] Trial 47 finished with value: 3023.676025390625 and parameters: {'eta': 0.16467209050245155, 'max_depth': 4, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 3.230462326784356, 'min_sum_hessian_in_leaf': 1.1106443915756805, 'subsample': 0.8624551086972744, 'feature_fraction': 0.45067165580000546, 'boosting': 'gbdt'}. Best is trial 35 with value: 3000.99462890625.
[I 2023-08-11 12:55:32,412] Trial 48 pruned. Trial was pruned at iteration 20.
[I 2023-08-11 12:56:15,258] Trial 49 finished with value: 3001.418212890625 and parameters: {'eta': 0.08071812906410179, 'max_depth': 3, 'num_leaves': 255, 'min_data_in_leaf': 20, 'min_gain_to_split': 4.294318716703948, 'min_sum_hessian_in_leaf': 2.6750545089295956, 'subsample': 0.9632339172694735, 'feature_fraction': 0.5074780056230868, 'boosting': 'gbdt'}. Best is trial 35 with value: 3000.99462890625.
Hyper-Parameter Optimization successfully finished.
Number of finished trials: 50
Best trial:
Value: 3000.99462890625
Params:
eta: 0.06943267180218958
max_depth: 4
num_leaves: 255
min_data_in_leaf: 20
min_gain_to_split: 4.133726741234719
min_sum_hessian_in_leaf: 1.7385973286087377
subsample: 0.8908962112260067
feature_fraction: 0.42160506776781076
boosting: gbdt
opt_rounds: 90
Model Training¶
In [18]:
Copied!
np.random.seed(123)
opt_params = opt_param.copy()
n_rounds = opt_params["opt_rounds"]
del opt_params["opt_rounds"]
# Train Model with optimized hyperparameters
lgblss.train(opt_params,
dtrain,
num_boost_round=n_rounds
)
np.random.seed(123)
opt_params = opt_param.copy()
n_rounds = opt_params["opt_rounds"]
del opt_params["opt_rounds"]
# Train Model with optimized hyperparameters
lgblss.train(opt_params,
dtrain,
num_boost_round=n_rounds
)
Prediction¶
In [19]:
Copied!
# Set seed for reproducibility
torch.manual_seed(123)
# Number of samples to draw from predicted distribution
n_samples = 10000
# Quantiles to calculate from predicted distribution
quant_sel = [0.05, 0.95]
# Sample from predicted distribution
pred_samples = lgblss.predict(X_test,
pred_type="samples",
n_samples=n_samples,
seed=123)
# Calculate quantiles from predicted distribution
pred_quantiles = lgblss.predict(X_test,
pred_type="quantiles",
n_samples=n_samples,
quantiles=quant_sel)
# Returns predicted parameters
pred_params = lgblss.predict(X_test,
pred_type="parameters")
# Set seed for reproducibility
torch.manual_seed(123)
# Number of samples to draw from predicted distribution
n_samples = 10000
# Quantiles to calculate from predicted distribution
quant_sel = [0.05, 0.95]
# Sample from predicted distribution
pred_samples = lgblss.predict(X_test,
pred_type="samples",
n_samples=n_samples,
seed=123)
# Calculate quantiles from predicted distribution
pred_quantiles = lgblss.predict(X_test,
pred_type="quantiles",
n_samples=n_samples,
quantiles=quant_sel)
# Returns predicted parameters
pred_params = lgblss.predict(X_test,
pred_type="parameters")
In [20]:
Copied!
pred_samples.head()
pred_samples.head()
Out[20]:
| y_sample0 | y_sample1 | y_sample2 | y_sample3 | y_sample4 | y_sample5 | y_sample6 | y_sample7 | y_sample8 | y_sample9 | ... | y_sample9990 | y_sample9991 | y_sample9992 | y_sample9993 | y_sample9994 | y_sample9995 | y_sample9996 | y_sample9997 | y_sample9998 | y_sample9999 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 12.315617 | 11.148891 | 4.624041 | 11.273465 | 4.864611 | 13.651609 | 11.573423 | 14.295194 | 9.939115 | 8.728693 | ... | 13.490867 | 9.317229 | 8.216475 | 11.480260 | 9.670330 | 14.858524 | 5.511271 | 10.839365 | 11.708204 | 6.417930 |
| 1 | 16.409412 | 8.340928 | 10.923915 | 13.388198 | 8.266445 | 10.249456 | 12.452267 | 10.588787 | 12.331830 | 9.027943 | ... | 10.883108 | 2.895114 | 11.342189 | 13.237988 | 6.858677 | 15.392724 | 9.221172 | 9.709686 | 4.011642 | 10.250503 |
| 2 | 11.589569 | 9.669224 | 9.724932 | 10.960885 | 13.362031 | 11.276797 | 10.801574 | 9.534609 | 9.327179 | 10.494802 | ... | 10.138949 | 11.022624 | 8.731875 | 10.401649 | 9.127348 | 10.243149 | 9.944046 | 8.483890 | 10.321774 | 10.243544 |
| 3 | 10.743192 | 9.116656 | 12.323032 | 5.270192 | 15.528632 | 15.910578 | 8.639240 | 16.705225 | 7.853291 | 9.957293 | ... | 1.351381 | 9.039200 | 16.516144 | 8.261804 | 4.777587 | 9.089480 | 12.751478 | 12.829519 | 12.620325 | 9.282865 |
| 4 | 12.725435 | 8.629576 | 7.140886 | 5.782235 | 6.844902 | 10.355301 | 7.330880 | 14.259795 | 10.242219 | 15.360129 | ... | 9.775837 | 8.244545 | 9.040227 | 11.909575 | 8.996835 | 8.084206 | 13.316805 | 10.463615 | 8.097854 | 9.440963 |
5 rows × 10000 columns
In [21]:
Copied!
pred_quantiles.head()
pred_quantiles.head()
Out[21]:
| quant_0.05 | quant_0.95 | |
|---|---|---|
| 0 | 5.220628 | 14.963007 |
| 1 | 5.365820 | 15.105494 |
| 2 | 8.211895 | 11.933730 |
| 3 | 2.047034 | 17.560992 |
| 4 | 5.048092 | 15.145446 |
In [22]:
Copied!
pred_params.head()
pred_params.head()
Out[22]:
| param_1 | param_2 | param_3 | param_4 | param_5 | param_6 | param_7 | param_8 | param_9 | param_10 | ... | param_22 | param_23 | param_24 | param_25 | param_26 | param_27 | param_28 | param_29 | param_30 | param_31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -0.418612 | -0.302259 | -0.532314 | -0.775419 | 0.697199 | -0.227767 | -3.043896 | 1.286783 | 1.113216 | 0.349978 | ... | 1.817143 | 0.570572 | 0.945506 | 0.805746 | 0.693497 | 0.639612 | 1.854735 | 1.306370 | 0.909254 | 0.839281 |
| 1 | -0.418612 | -0.302259 | -0.532314 | -0.775419 | 0.697199 | -0.227767 | -3.043896 | 1.286783 | 1.113216 | 0.349978 | ... | 1.777844 | 0.570572 | 0.945506 | 0.805746 | 0.693497 | 0.639612 | 1.854735 | 1.306370 | 0.909254 | 0.839281 |
| 2 | -0.418612 | -0.302259 | -0.532314 | -0.775419 | 0.697199 | -0.227767 | -3.043896 | 1.286783 | 1.113216 | 0.349978 | ... | 1.495455 | 0.570572 | 0.945506 | 0.805746 | 0.693497 | 0.639612 | 0.868014 | 2.313089 | 0.909254 | 0.839281 |
| 3 | -0.418612 | -0.302259 | -0.532314 | -0.775419 | 0.697199 | -0.227767 | -3.043896 | 1.286783 | 1.113216 | 0.349978 | ... | 1.276525 | 0.570572 | 0.945506 | 0.805746 | 0.693497 | 0.639612 | 2.172172 | -1.196684 | 0.909254 | 0.839281 |
| 4 | -0.418612 | -0.302259 | -0.532314 | -0.775419 | 0.697199 | -0.227767 | -3.043896 | 1.286783 | 1.113216 | 0.349978 | ... | 1.535858 | 0.570572 | 0.945506 | 0.805746 | 0.693497 | 0.639612 | 1.854735 | 1.127365 | 0.909254 | 0.839281 |
5 rows × 31 columns
SHAP Interpretability¶
Note that in contrast to parametric distributions, the parameters of the Spline-Flow do not have a direct interpretation.
In [23]:
Copied!
# Partial Dependence Plot of how x acts on param_21
lgblss.plot(X_test,
parameter="param_21",
feature="x_true",
plot_type="Partial_Dependence")
# Partial Dependence Plot of how x acts on param_21
lgblss.plot(X_test,
parameter="param_21",
feature="x_true",
plot_type="Partial_Dependence")
In [24]:
Copied!
# Feature Importance of param_21
lgblss.plot(X_test,
parameter="param_21",
plot_type="Feature_Importance")
# Feature Importance of param_21
lgblss.plot(X_test,
parameter="param_21",
plot_type="Feature_Importance")
Plot of Actual vs. Predicted Quantiles¶
In [25]:
Copied!
np.random.seed(123)
###
# Actual Quantiles
###
q1 = norm.ppf(quant_sel[0], loc = 10, scale = 1 + 4*((0.3 < test["x_true"].values) & (test["x_true"].values < 0.5)) + 2*(test["x_true"].values > 0.7))
q2 = norm.ppf(quant_sel[1], loc = 10, scale = 1 + 4*((0.3 < test["x_true"].values) & (test["x_true"].values < 0.5)) + 2*(test["x_true"].values > 0.7))
test["quant"] = np.where(test["y"].values < q1, 0, np.where(test["y"].values < q2, 1, 2))
test["alpha"] = np.where(test["y"].values <= q1, 1, np.where(test["y"].values >= q2, 1, 0))
df_quantiles = test[test["alpha"] == 1]
# Lower Bound
yl = list(set(q1))
yl.sort()
yl = [yl[2],yl[0],yl[2],yl[1],yl[1]]
sfunl = pd.DataFrame({"x_true":[0, 0.3, 0.5, 0.7, 1], "y":yl})
# Upper Bound
yu = list(set(q2))
yu.sort()
yu = [yu[0],yu[2],yu[0],yu[1],yu[1]]
sfunu = pd.DataFrame({"x_true":[0, 0.3, 0.5, 0.7, 1], "y":yu})
###
# Predicted Quantiles
###
test["lb"] = pred_quantiles.iloc[:,0]
test["ub"] = pred_quantiles.iloc[:,1]
###
# Plot
###
(ggplot(test,
aes("x_true",
"y")) +
geom_point(alpha = 0.2, color = "black", size = 2) +
theme_bw(base_size=15) +
theme(legend_position="none",
plot_title = element_text(hjust = 0.5)) +
labs(title = "LightGBMLSS Regression - Simulated Data Example",
x="x") +
geom_line(aes("x_true",
"ub"),
size = 1,
color = "blue",
alpha = 0.7) +
geom_line(aes("x_true",
"lb"),
size = 1,
color = "blue",
alpha = 0.7) +
geom_point(df_quantiles,
aes("x_true",
"y"),
color = "red",
alpha = 0.7,
size = 2) +
geom_step(sfunl,
aes("x_true",
"y"),
size = 1,
linetype = "dashed") +
geom_step(sfunu,
aes("x_true",
"y"),
size = 1,
linetype = "dashed")
)
np.random.seed(123)
###
# Actual Quantiles
###
q1 = norm.ppf(quant_sel[0], loc = 10, scale = 1 + 4*((0.3 < test["x_true"].values) & (test["x_true"].values < 0.5)) + 2*(test["x_true"].values > 0.7))
q2 = norm.ppf(quant_sel[1], loc = 10, scale = 1 + 4*((0.3 < test["x_true"].values) & (test["x_true"].values < 0.5)) + 2*(test["x_true"].values > 0.7))
test["quant"] = np.where(test["y"].values < q1, 0, np.where(test["y"].values < q2, 1, 2))
test["alpha"] = np.where(test["y"].values <= q1, 1, np.where(test["y"].values >= q2, 1, 0))
df_quantiles = test[test["alpha"] == 1]
# Lower Bound
yl = list(set(q1))
yl.sort()
yl = [yl[2],yl[0],yl[2],yl[1],yl[1]]
sfunl = pd.DataFrame({"x_true":[0, 0.3, 0.5, 0.7, 1], "y":yl})
# Upper Bound
yu = list(set(q2))
yu.sort()
yu = [yu[0],yu[2],yu[0],yu[1],yu[1]]
sfunu = pd.DataFrame({"x_true":[0, 0.3, 0.5, 0.7, 1], "y":yu})
###
# Predicted Quantiles
###
test["lb"] = pred_quantiles.iloc[:,0]
test["ub"] = pred_quantiles.iloc[:,1]
###
# Plot
###
(ggplot(test,
aes("x_true",
"y")) +
geom_point(alpha = 0.2, color = "black", size = 2) +
theme_bw(base_size=15) +
theme(legend_position="none",
plot_title = element_text(hjust = 0.5)) +
labs(title = "LightGBMLSS Regression - Simulated Data Example",
x="x") +
geom_line(aes("x_true",
"ub"),
size = 1,
color = "blue",
alpha = 0.7) +
geom_line(aes("x_true",
"lb"),
size = 1,
color = "blue",
alpha = 0.7) +
geom_point(df_quantiles,
aes("x_true",
"y"),
color = "red",
alpha = 0.7,
size = 2) +
geom_step(sfunl,
aes("x_true",
"y"),
size = 1,
linetype = "dashed") +
geom_step(sfunu,
aes("x_true",
"y"),
size = 1,
linetype = "dashed")
)
Out[25]:
<Figure Size: (2000 x 1000)>
True vs. Predicted Distributional Parameters¶
In the following figure, we compare the true parameters of the Gaussian with the ones predicted by LightGBMLSS. The below figure shows that the estimated parameters closely match the true ones (recall that the location parameter $\mu=10$ is simulated as being a constant).
In [26]:
Copied!
dist_params = ["loc", "scale"]
# Calculate parameters from samples
sample_params = pd.DataFrame.from_dict(
{
"loc": pred_samples.mean(axis=1),
"scale": pred_samples.std(axis=1),
"x_true": X_test["x_true"].values
}
)
# Data with predicted values
plot_df_predt = pd.melt(sample_params[["x_true"] + dist_params],
id_vars="x_true",
value_vars=dist_params)
plot_df_predt["type"] = "PREDICT"
# Data with actual values
plot_df_actual = pd.melt(test[["x_true"] + dist_params],
id_vars="x_true",
value_vars=dist_params)
plot_df_actual["type"] = "TRUE"
# Combine data for plotting
plot_df = pd.concat([plot_df_predt, plot_df_actual])
plot_df["variable"] = plot_df.variable.str.upper()
plot_df["type"] = pd.Categorical(plot_df["type"], categories = ["PREDICT", "TRUE"])
# Plot
(ggplot(plot_df,
aes(x="x_true",
y="value",
color="type")) +
geom_line(size=1.1) +
facet_wrap("variable",
scales="free") +
labs(title="Parameters of univariate Gaussian predicted with LightGBMLSS",
x="",
y="") +
theme_bw(base_size=15) +
theme(legend_position="bottom",
plot_title = element_text(hjust = 0.5),
legend_title = element_blank())
)
dist_params = ["loc", "scale"]
# Calculate parameters from samples
sample_params = pd.DataFrame.from_dict(
{
"loc": pred_samples.mean(axis=1),
"scale": pred_samples.std(axis=1),
"x_true": X_test["x_true"].values
}
)
# Data with predicted values
plot_df_predt = pd.melt(sample_params[["x_true"] + dist_params],
id_vars="x_true",
value_vars=dist_params)
plot_df_predt["type"] = "PREDICT"
# Data with actual values
plot_df_actual = pd.melt(test[["x_true"] + dist_params],
id_vars="x_true",
value_vars=dist_params)
plot_df_actual["type"] = "TRUE"
# Combine data for plotting
plot_df = pd.concat([plot_df_predt, plot_df_actual])
plot_df["variable"] = plot_df.variable.str.upper()
plot_df["type"] = pd.Categorical(plot_df["type"], categories = ["PREDICT", "TRUE"])
# Plot
(ggplot(plot_df,
aes(x="x_true",
y="value",
color="type")) +
geom_line(size=1.1) +
facet_wrap("variable",
scales="free") +
labs(title="Parameters of univariate Gaussian predicted with LightGBMLSS",
x="",
y="") +
theme_bw(base_size=15) +
theme(legend_position="bottom",
plot_title = element_text(hjust = 0.5),
legend_title = element_blank())
)
Out[26]:
<Figure Size: (2000 x 1000)>
Density Plots¶
In [27]:
Copied!
pred_df = pd.melt(pred_samples.iloc[:,0:5])
actual_df = pd.DataFrame.from_dict({"variable": "ACTUAL", "value": y_test.reshape(-1,)})
plot_df = pd.concat([pred_df, actual_df])
(
ggplot(plot_df,
aes(x="value",
color="variable",
fill="variable")) +
geom_density(alpha=0.4) +
facet_wrap("variable",
ncol=2) +
theme_bw(base_size=15) +
theme(plot_title = element_text(hjust = 0.5)) +
theme(legend_position="none")
)
pred_df = pd.melt(pred_samples.iloc[:,0:5])
actual_df = pd.DataFrame.from_dict({"variable": "ACTUAL", "value": y_test.reshape(-1,)})
plot_df = pd.concat([pred_df, actual_df])
(
ggplot(plot_df,
aes(x="value",
color="variable",
fill="variable")) +
geom_density(alpha=0.4) +
facet_wrap("variable",
ncol=2) +
theme_bw(base_size=15) +
theme(plot_title = element_text(hjust = 0.5)) +
theme(legend_position="none")
)
Out[27]:
<Figure Size: (2000 x 1000)>
Actual vs. Predicted¶
Since we predict the entire conditional distribution, we can overlay the point predictions with predicted densities, from which we can also derive quantiles of interest.
In [28]:
Copied!
y_pred = []
n_examples = 8
q_sel = [0.05, 0.95]
y_sel=0
samples_arr = pred_samples.values.reshape(-1,n_samples)
for i in range(n_examples):
y_samples = pd.DataFrame(samples_arr[i,:].reshape(-1,1), columns=["PREDICT_DENSITY"])
y_samples["PREDICT_POINT"] = y_samples["PREDICT_DENSITY"].mean()
y_samples["PREDICT_Q05"] = y_samples["PREDICT_DENSITY"].quantile(q=q_sel[0])
y_samples["PREDICT_Q95"] = y_samples["PREDICT_DENSITY"].quantile(q=q_sel[1])
y_samples["ACTUAL"] = y_test[i]
y_samples["obs"]= f"Obervation {i+1}"
y_pred.append(y_samples)
pred_df = pd.melt(pd.concat(y_pred, axis=0), id_vars="obs")
pred_df["obs"] = pd.Categorical(pred_df["obs"], categories=[f"Obervation {i+1}" for i in range(n_examples)])
df_actual, df_pred_dens, df_pred_point, df_q05, df_q95 = [x for _, x in pred_df.groupby("variable")]
plot_pred = (
ggplot(pred_df,
aes(color="variable")) +
stat_density(df_pred_dens,
aes(x="value"),
size=1.1) +
geom_point(df_pred_point,
aes(x="value",
y=0),
size=1.4) +
geom_point(df_actual,
aes(x="value",
y=0),
size=1.4) +
geom_vline(df_q05,
aes(xintercept="value",
fill="variable",
color="variable"),
linetype="dashed",
size=1.1) +
geom_vline(df_q95,
aes(xintercept="value",
fill="variable",
color="variable"),
linetype="dashed",
size=1.1) +
facet_wrap("obs",
scales="free",
ncol=4) +
labs(title="Predicted vs. Actual \n",
x = "") +
theme_bw(base_size=15) +
theme(plot_title = element_text(hjust = 0.5)) +
scale_fill_brewer(type="qual", palette="Dark2") +
theme(legend_position="bottom",
legend_title = element_blank()
)
)
print(plot_pred)
y_pred = []
n_examples = 8
q_sel = [0.05, 0.95]
y_sel=0
samples_arr = pred_samples.values.reshape(-1,n_samples)
for i in range(n_examples):
y_samples = pd.DataFrame(samples_arr[i,:].reshape(-1,1), columns=["PREDICT_DENSITY"])
y_samples["PREDICT_POINT"] = y_samples["PREDICT_DENSITY"].mean()
y_samples["PREDICT_Q05"] = y_samples["PREDICT_DENSITY"].quantile(q=q_sel[0])
y_samples["PREDICT_Q95"] = y_samples["PREDICT_DENSITY"].quantile(q=q_sel[1])
y_samples["ACTUAL"] = y_test[i]
y_samples["obs"]= f"Obervation {i+1}"
y_pred.append(y_samples)
pred_df = pd.melt(pd.concat(y_pred, axis=0), id_vars="obs")
pred_df["obs"] = pd.Categorical(pred_df["obs"], categories=[f"Obervation {i+1}" for i in range(n_examples)])
df_actual, df_pred_dens, df_pred_point, df_q05, df_q95 = [x for _, x in pred_df.groupby("variable")]
plot_pred = (
ggplot(pred_df,
aes(color="variable")) +
stat_density(df_pred_dens,
aes(x="value"),
size=1.1) +
geom_point(df_pred_point,
aes(x="value",
y=0),
size=1.4) +
geom_point(df_actual,
aes(x="value",
y=0),
size=1.4) +
geom_vline(df_q05,
aes(xintercept="value",
fill="variable",
color="variable"),
linetype="dashed",
size=1.1) +
geom_vline(df_q95,
aes(xintercept="value",
fill="variable",
color="variable"),
linetype="dashed",
size=1.1) +
facet_wrap("obs",
scales="free",
ncol=4) +
labs(title="Predicted vs. Actual \n",
x = "") +
theme_bw(base_size=15) +
theme(plot_title = element_text(hjust = 0.5)) +
scale_fill_brewer(type="qual", palette="Dark2") +
theme(legend_position="bottom",
legend_title = element_blank()
)
)
print(plot_pred)
